FFT

Fast Fourier transformation.

Format:

SPECTRA> fft id1 [id2]

Description:

A fast Fourier transformation (code from Numerical Recipes) is done on id1. If id2 is supplied, the transformed SCAN has the name id2_f, otherwise id1_f. The number of points of id1 must be a power of two. That can be easily achieved by the command

SPECTRA> smooth/s=0/np=power-of-two ...

or by adding equidistant zeros:

SPECTRA> create zero 0 25000 255 0
SPECTRA> calc bpu1 = zero + bpu1

/low=val1, /high=val2

The cuts are imposed on the transformed distribution. A back-transformation is performed which created the SCAN id2_ff or id1_ff.

e.g.:

SPECTRA> smooth/s=0/np=256 bpu1

SPECTRA> fft /low=0.001/high=0.003 bpu1_s

The FFT command produces a frequency spectrum from a time distribution. In fact it is the square root of the sum of the squares of the Fourier coefficients, which belong to positive frequencies.

Suppose you measure n points, the time interval being delta. The Fourier transformation will produce n complex coefficients which belong to the frequency interval from -Fc to Fc (Fc = 1 / (2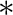$*$delta)). The coefficients are squared and since they are symmetrical with respect to the y-axis (c(-f) = c(f)), only the +f part is given to the user (id2_f).

If the user applies cuts to the frequency function, it is re-transformed to a time-function. This way the user does not have to deal with the coefficients.